TensorFlow-平面曲线拟合

平面曲线属于非线性函数，至少需要 3 层的神经网络（输入层，隐藏层x1，输出层）来实现，为达到较好的效果，可尝试更多层，下面的例子使用了2层隐藏层，采用最基本的全连接形式，隐藏层的神经元个数没有严格要求，根据实际项目选择，下面例子选用8个。

下面通过代码实现：

引入相关库，定义神经网络层

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 构造添加一个神经层的函数
def add_layer(inputs, in_size, out_size, activation_function=None):
    Weights = tf.Variable(tf.random_normal([in_size, out_size])) #权重矩阵[列，行]
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) # 偏置向量[列，行]
    Wx_plus_b = tf.matmul(inputs, Weights) + biases # w*x+b(未激活)
    if activation_function is None: # 线性关系（不使用激活函数）
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)# 非线性激活
    return outputs

生成些输入数据并导入网路

因为要拟合平面曲线，输入x和输出y均为一维数据

# 导入数据，这里的x_data和y_data并不是严格的一元二次函数的关系
# 因为我们多加了一个noise,这样看起来会更像真实情况
x_data = np.linspace(-1,1,300, dtype=np.float32)[:, np.newaxis]#300行，1个特性
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)# 均值，方差，形状 
y_data = np.power(x_data,3)*10 - 8*noise # y = x^2-0.5+noise

# 利用占位符定义我们所需的神经网络的输入
# None代表无论输入有多少都可以，因为输入只有一个特征，所以这里是1
xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])

搭建网络
输入层：神经元个数1(输出1)

隐藏层1：神经元个数8(输入1，输出8)

隐藏层2：神经元个数8(输入8，输出8)

输出层：神经元个数1(输入8，输出1)

# 定义隐藏层【l1】和【l2】,利用之前的add_layer()函数
l1 = add_layer(xs, 1, 8, activation_function=tf.nn.sigmoid) # 输入层，输入，输出
l2 = add_layer(l1, 8, 8, activation_function=tf.nn.sigmoid) # 输入层，输入，输出

# 定义输出层【prediction】。输入就是隐藏层的输出——l1，输入有10层，输出有1层
prediction = add_layer(l2, 8, 1, activation_function=None)

损失函数

1 2	# 计算预测值prediction和真实值的误差，对二者差的平方求和再取平均 loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),reduction_indices=[1]))

梯度下降法

1
2
3

# tf.train.GradientDescentOptimizer()中的值通常都小于1，
# 这里取的是0.08，学习率，代表以0.08的效率来最小化误差loss
train_step = tf.train.GradientDescentOptimizer(0.08).minimize(loss)

训练前的初始化操作

# 使用变量时，都要对它进行初始化
init = tf.global_variables_initializer()

# 定义Session，并用 Session 来执行 init 初始化步骤
sess = tf.Session()
sess.run(init)

使用matplotlib可视化结果

fig = plt.figure() #先生成一个图片框
ax = fig.add_subplot(1,1,1)#子图位置
ax.scatter(x_data,y_data,c = 'b',marker = '.')
plt.ion() # plt.ion()用于连续显示

训练过程

# 学习1000次。学习内容是train_step, 用Session来run每一次training的数据
for i in range(1000):
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})

    # 每50步我们输出一下机器学习的误差
    if i % 50 == 0:
        print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))
        try:
             ax.lines.remove(lines[0]) #抹除上一次的第一条线（总共就一条）
        except Exception:
            pass    
        prediction_value = sess.run(prediction,feed_dict={xs:x_data})
        # plot the prediction
        lines = ax.plot(x_data,prediction_value,'r-',lw=5)
        plt.pause(0.2)

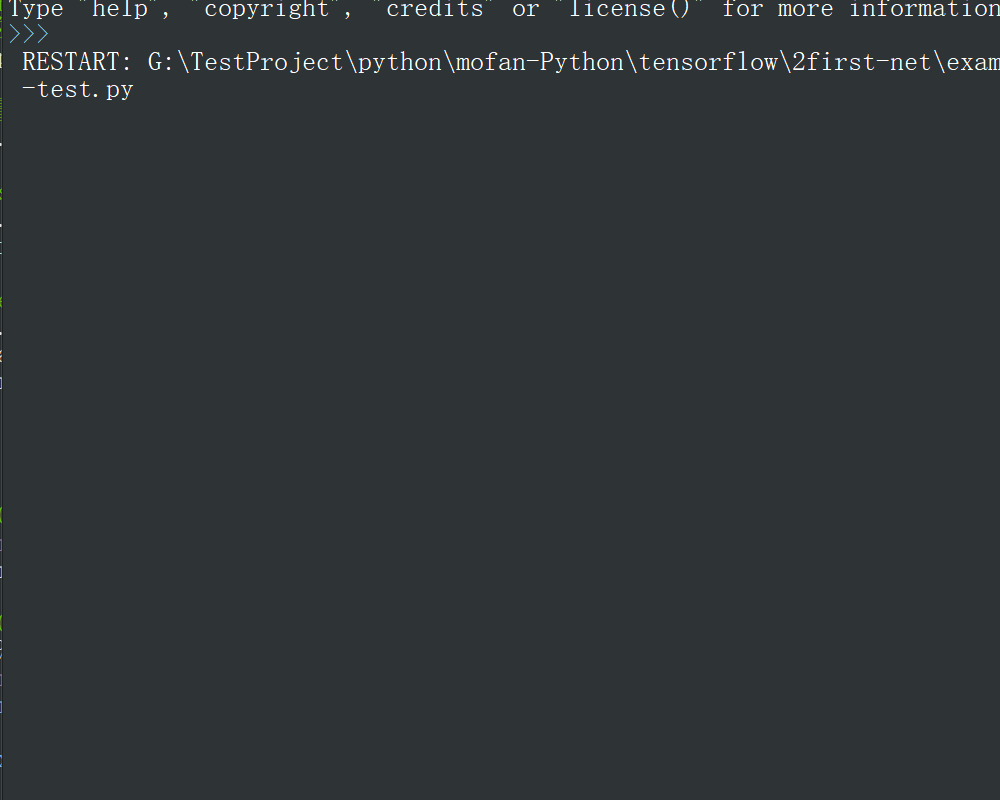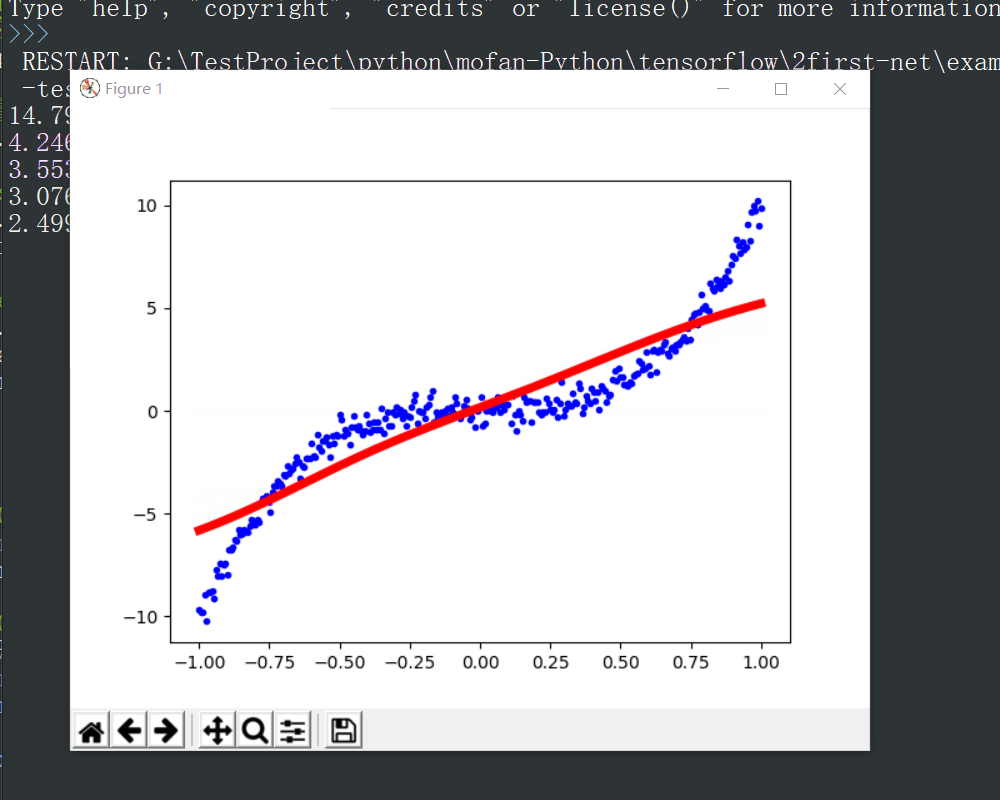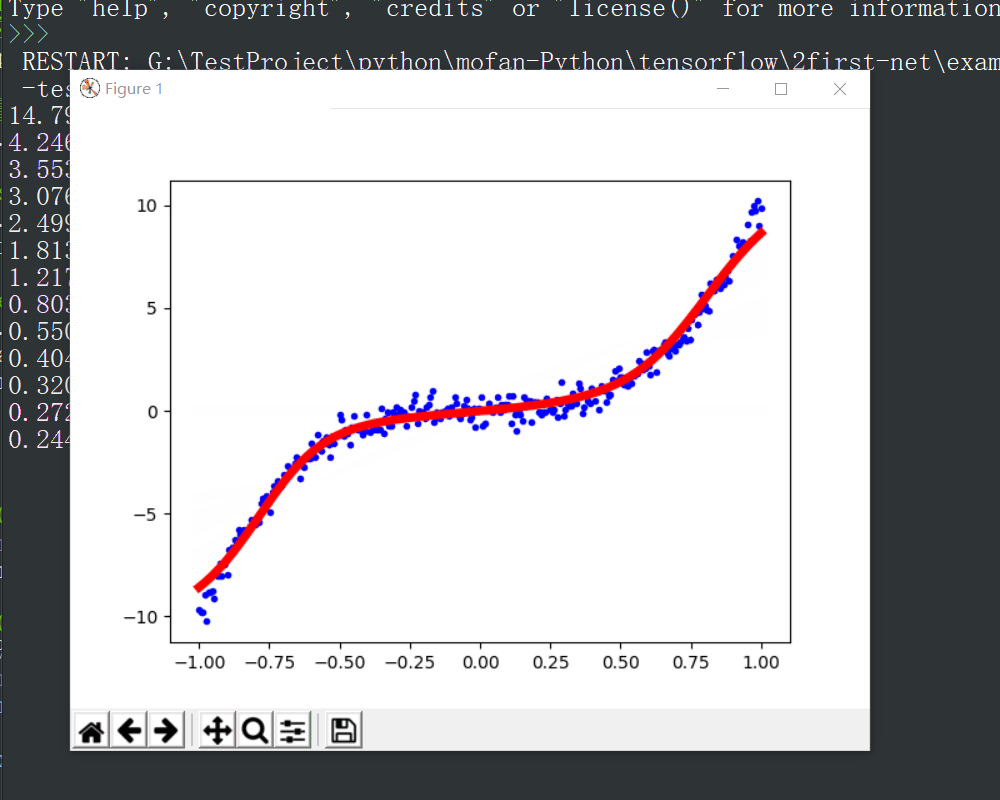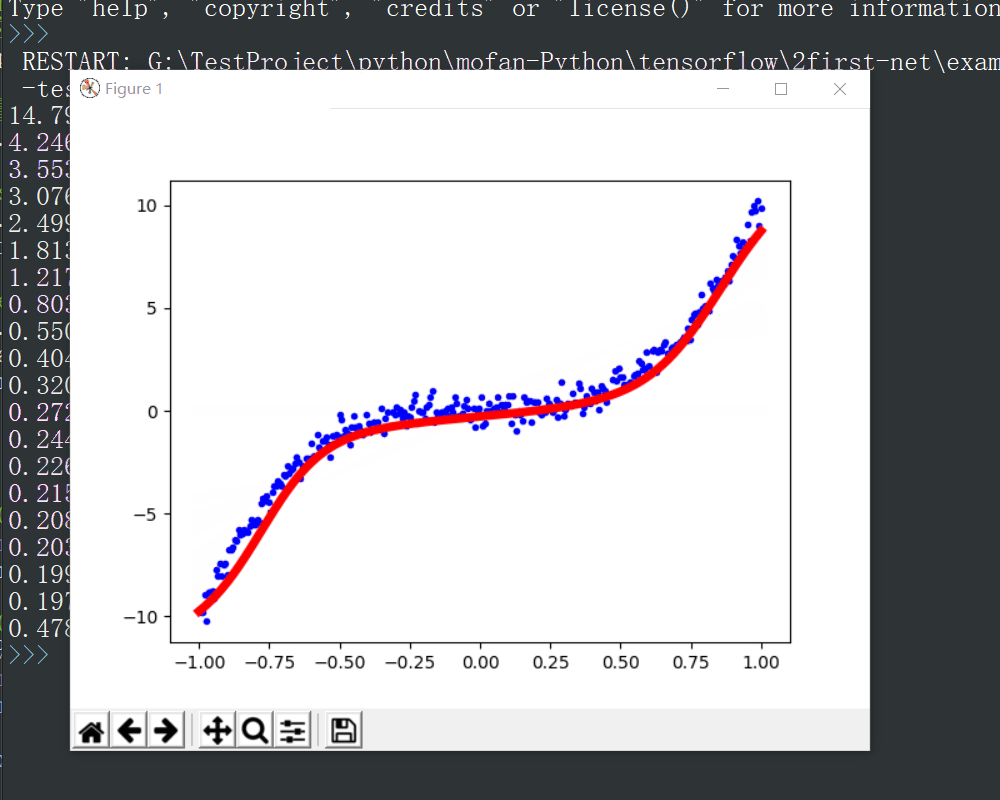
运行结果

可以看出，随着训练的进行，损失函数的值不断减小，同时拟合出的结果（红线）不断接近原始训练数据（蓝点），增加训练次数可以提高拟合精度。

注意，每次运行的结果会略有不同，下图结果在最后一轮显示时出现了跳变，同时损失函数值略有增加，原因在于训练参数没有始终朝着最优变化，会有一些抖动，可能是梯度下降时到达某个局部最小点后又向外跳出，可通过重新训练、增加训练次数或调整学习率等方式解决。