3维旋转矩阵推导与助记
旋转矩阵的应用范围比较广,是姿态变换,坐标变换等的基础。本篇先介绍旋转矩阵的推导过程与助记方法。
平面二维旋转
如下图,XY坐标系中,向量OP旋转β角度到了OP’的位置:
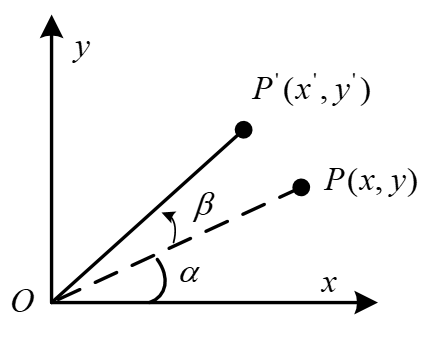
根据三角函数关系,可以列出向量OP与OP’的坐标表示形式:
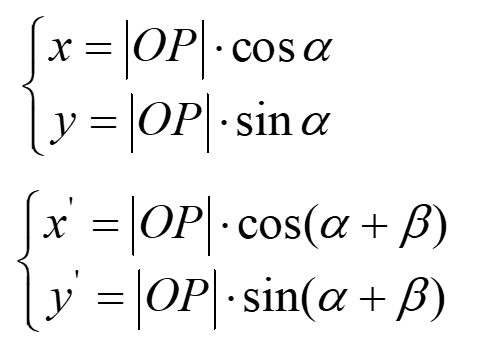
对比上面个两个式子,将第2个式子展开:
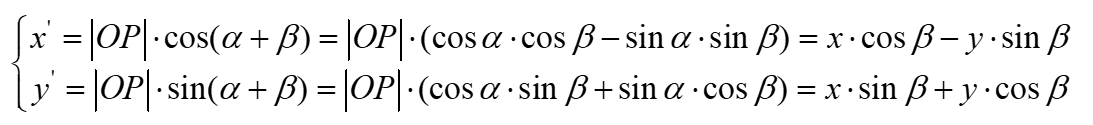
用矩阵形式重新表示为:

这就是二维旋转的基本形式,中间的矩阵即二维旋转的旋转矩阵,坐标中的某一向量左乘该矩阵后,即得到这个向量旋转β角后的坐标。
三维旋转
三维旋转可借助二维旋转来理解,由于三维空间中可以任意轴旋转,为方便分析与使用,只考虑绕X、Y、Z轴的旋转。
绕Z轴
参照上面的图,添加一个Z轴,则上面的二维旋转实际上就是绕Z轴的三维旋转
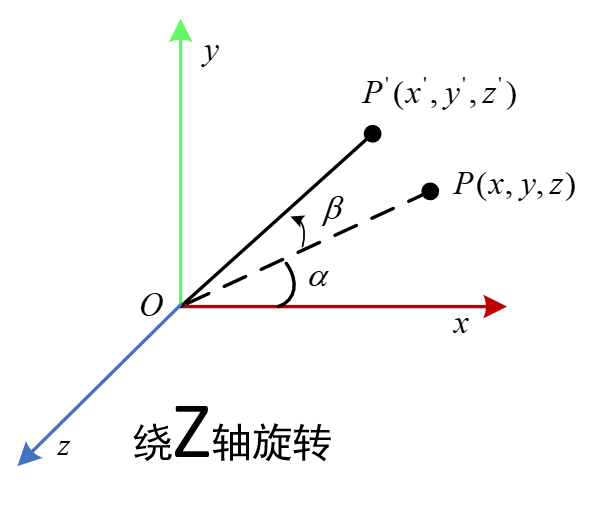
照搬上面的推导公式,并添加Z坐标的变换关系(实际是没有变),然后改写成矩阵形式,红色方框即为绕Z轴的旋转矩阵。
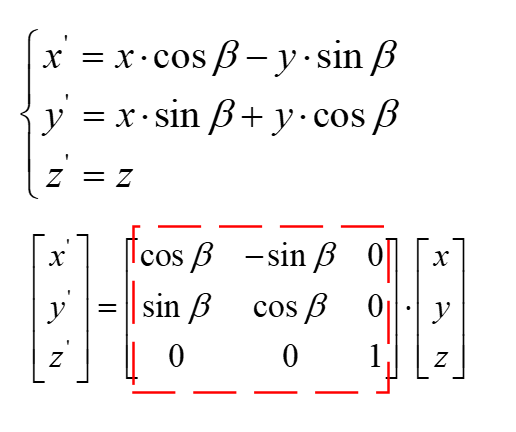
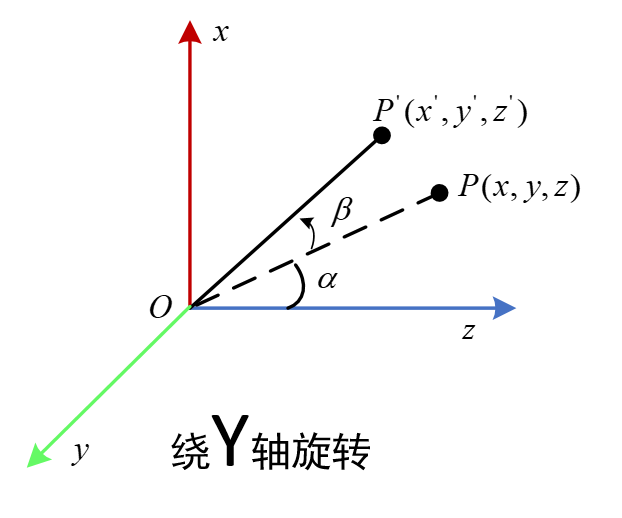
绕Y轴
绕Y轴旋转同理,这里直接改变坐标轴的符号表示,注意坐标顺序要符合右手系,我这里用颜色区分了不同的轴。最终的矩阵形式要进一步改写成XYZ的顺序。红色方框即为绕Y轴的旋转矩阵。
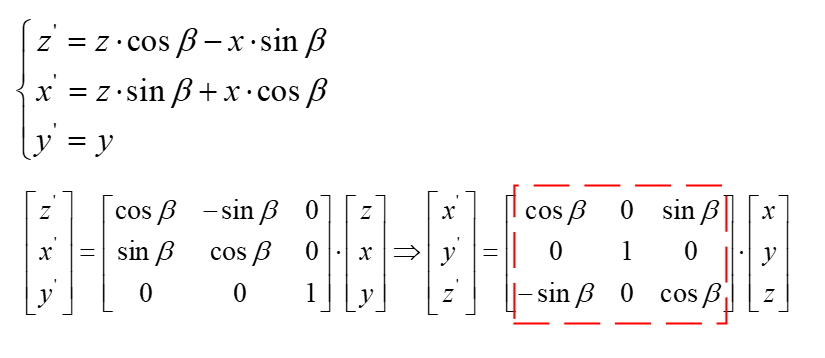
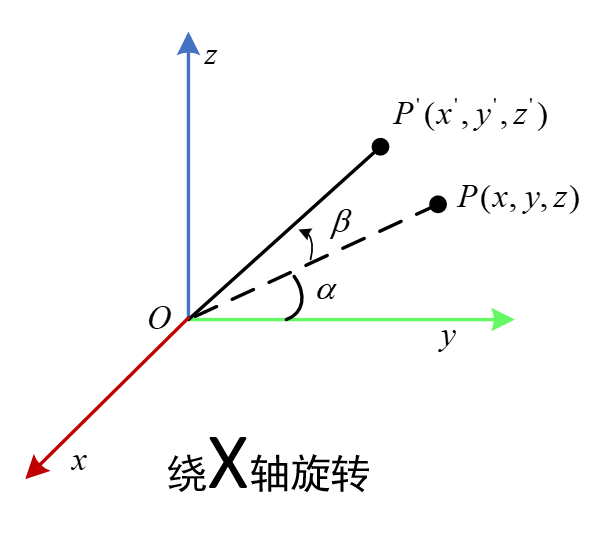
绕X轴
参照绕Y轴的推导,可以得到绕X轴的结果。红色方框即为绕X轴的旋转矩阵。

助记
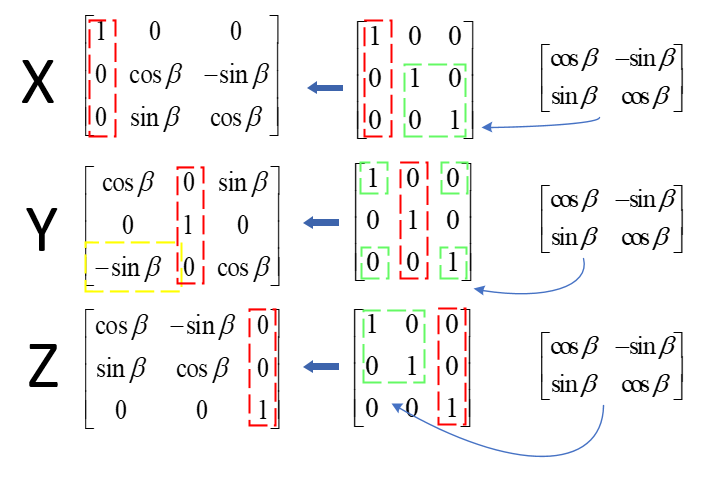
对于单位矩阵,绕哪个轴旋转,哪一列不用变,然后将二维旋转矩阵替换对应的4个位置,注意,绕Y的旋转矩阵看起来与另外两个不同,它的-sinβ是在左下!
注意事项
反向旋转
如果是反向旋转一个角度,推导过程类似:
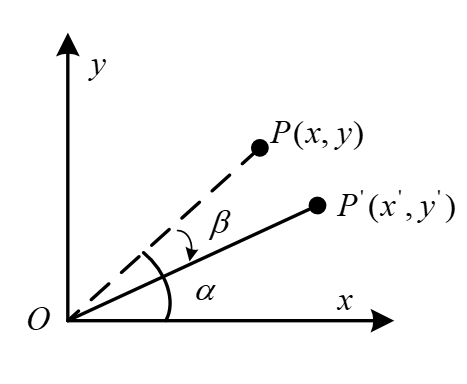
最终得到的旋转矩阵其实是正向旋转矩阵的逆矩阵,由于这个矩阵是正交阵,所以逆矩阵就是转置矩阵。
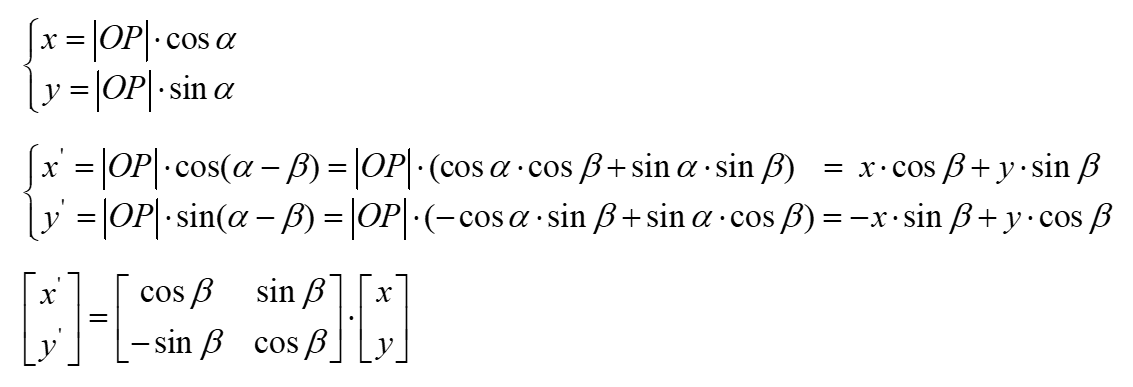
书写形式
上面的向量的坐标都是按照列的形式书写,如果是换成行的形式表示,则旋转的矩阵形式被转置了一下,同时矩阵在行向量的右边进行相乘。
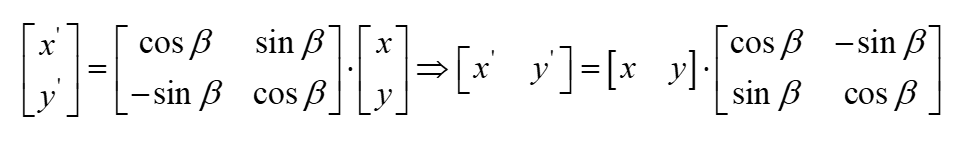
-------------纸短情长 下次再见-------------
关注微信公众号,获取更多精彩~
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 码农爱学习的博客!
评论







