欧拉角旋转
欧拉角是一种表示三维旋转的描述方法,欧拉角的计算需要借助旋转矩阵,关于旋转矩阵的知识可先参考前两篇文章:3维旋转矩阵推导与助记与3维旋转矩阵推导与助记-补充篇
欧拉角旋转
静态定义
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。
- 参考系又称为实验室参考系,是静止不动的,可以先简单的理解理解为大地坐标系,也称惯性坐标系。
- 坐标系则固定于刚体,随著刚体的旋转而旋转,比如飞行器自身的坐标系,也称载体坐标系。

如上图为一种ZYZ顺序旋转的欧拉角示意图:
- 设蓝色的xyz-轴为惯性系的参考轴,即大地坐标系的3个轴。
- 设红色的XYZ轴为载体系的参考轴,即飞行器坐标系的3个轴。
- 称xy-平面与XY-平面的相交为交点线,用英文字母N表示。
图中的角度符号:
α是x-轴与交点线的夹角,载体坐标系先绕Z轴旋转了α角度(范围0~2Pi弧度)。β是z-轴与Z-轴的夹角,载体坐标系又绕当前的Y轴旋转了β角度(范围0~Pi弧度)。γ是交点线与X-轴的夹角,载体坐标系又绕当前的Z轴旋转了γ角度(范围0~2Pi弧度)。- 这里角度的正负是按照右手定则,如右手大拇指指向z-轴,四指弯曲的旋转方向为α正方向。
其旋转动画为:
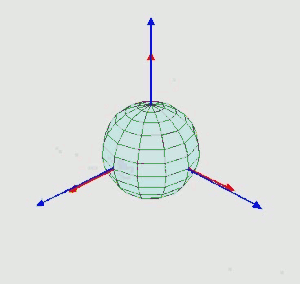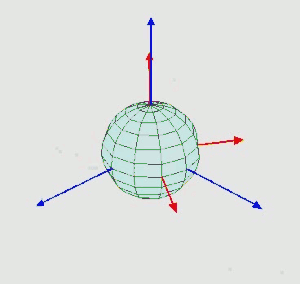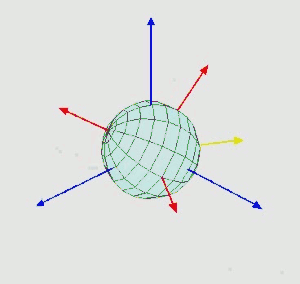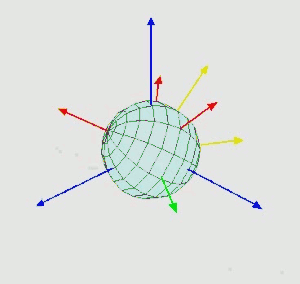
实际上,对于夹角的顺序和标记,夹角的两个轴的指定,并没有明确的规定。因此当用到欧拉角时,需要明确地表示出夹角的顺序,指定其参考轴。合法的欧拉角组中,唯一的限制是,任何两个连续的旋转,必须绕着不同的转动轴旋转。因此,一共有12种表示。
- 6种绕三条轴的旋转(Tait-Bryan Angle):XYZ, XZY, YXZ, YZX, ZXY, ZYX
- 6种只绕两条轴的旋转(Proper Euler Angle):XYX, YXY, XZX, ZXZ, YZY, ZYZ
动态定义
我们也可以给予欧拉角两种不同的动态定义。一种是绕固定于载体的坐标轴的三个旋转的复合;另外一种是绕大地坐标系参考轴的三个旋转的复合。
用动态的定义,我们能更了解,欧拉角在物理上的含义与应用。
注意,以下的描述, 大写字母XYZ坐标轴是旋转的载体坐标轴;小写字母xyz坐标轴是静止不动的大地参考轴。
现在以旋转顺序依次是Z、Y、X的方式来描述欧拉角的两种动态定义。
定义A:绕着XYZ坐标轴旋转(载体坐标轴):
- 最初,两个坐标系统xyz与XYZ的坐标轴都是重叠的。
- 开始,绕着Z-轴旋转α角度。
- 然后,绕着Y-轴旋转β角度。
- 最后,绕着X-轴旋转γ角度。
设任何一点P1在xyz与XYZ坐标系统的坐标分别为r1与R1。定义Z(α)为绕着Z-轴旋转α角度,Y(β)为绕着Y-轴旋转β角度,X(γ)为绕着X-轴旋转γ角度。则定义A可以表述如下:

注意这里又有矩阵左乘与右乘的概念,绕载体坐标系旋转是矩阵依次左乘,即X <- Y <- Z。
定义B:绕着xyz坐标轴旋转(大地坐标轴):
- 最初,两个坐标系统xyz与XYZ的坐标轴都是重叠的。
- 开始,绕着z-轴旋转α角度。
- 然后,绕着y-轴旋转β角度。
- 最后,绕着x-轴旋转γ角度。
设任何一点P2在xyz与XYZ坐标系统的坐标分别为r2与R2。定义z(α)为绕着z-轴旋转α角度,y(β)为绕着y-轴旋转β角度,x(γ)为绕着x-轴旋转γ角度。则定义B可以表述如下:
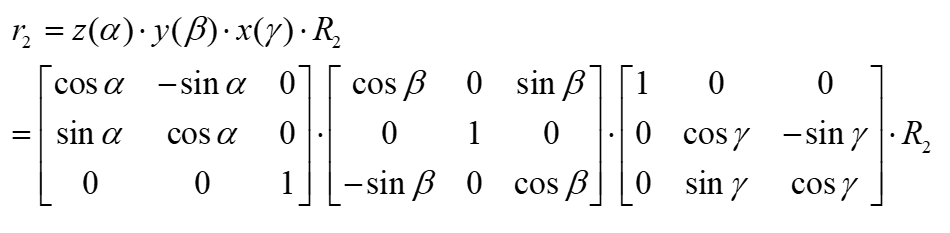
注意绕大地坐标系旋转是矩阵依次右乘,即z -> y -> x。
定义A与静态定义的相等,这可以直接用几何制图方法来核对。
定义A与定义B的相等可以用旋转矩阵来证明:








