3维旋转矩阵推导与助记-补充篇
这篇文章是对上篇3维旋转矩阵推导与助记的补充,上篇介绍的旋转矩阵是在同一个坐标系下,向量旋转所对应的旋转矩阵,本篇分析坐标系旋转对应的旋转矩阵。
平面二维旋转
如下图,xy坐标系中,有一向量OP,其坐标可表示为(x,y),该向量与X轴夹角为α。然后,坐标系绕原点逆时旋转了β角度,形成新的坐标系x’y’,此时OP在新的坐标系中的坐标表示为(x’,y’),根据几何关系,可以得到如下推导,最终得到绿色虚框的旋转矩阵。对比上篇文章的旋转矩阵,可以发现:本篇坐标系旋转的旋转矩阵与上篇向量旋转的旋转矩阵正好是转置的关系(实际上是逆矩阵,因为正交阵的逆矩阵与转置矩阵相同),因为这两种旋转本质上是相对运动,互为逆过程。
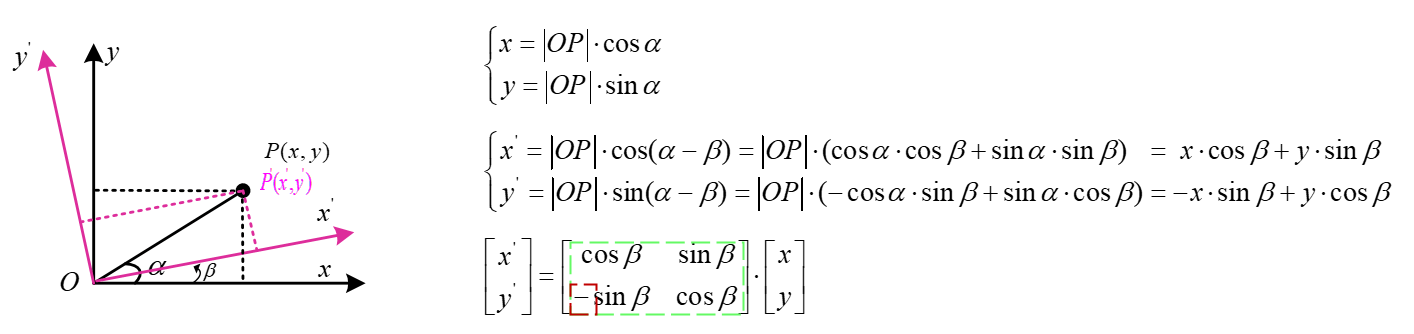
三维旋转
同样,三维情况下的坐标系旋转的旋转矩阵,与上篇向量旋转的旋转矩阵也是逆矩阵的关系,下面是绕3种轴的情况。
绕Z轴
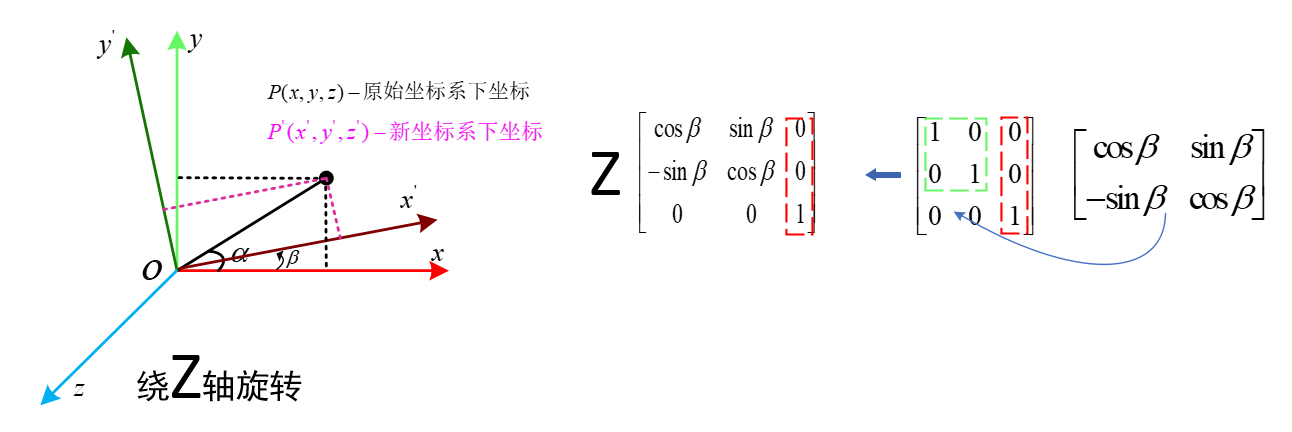
绕Y轴
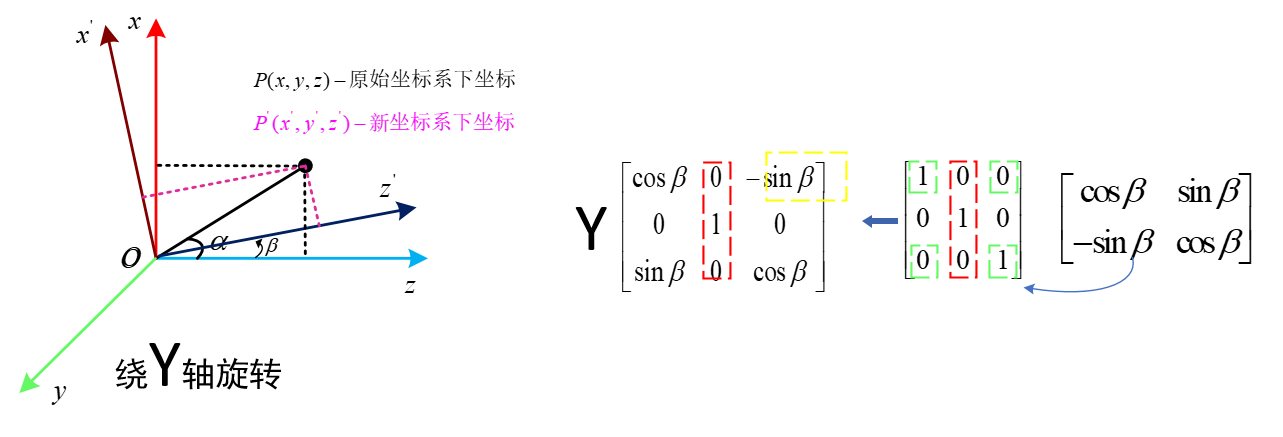
绕X轴

-------------纸短情长 下次再见-------------
关注微信公众号,获取更多精彩~
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 码农爱学习的博客!
评论







